On le dit souvent, en mathématiques, le cheminement importe plus que le résultat. Que l’on soit d’accord ou non avec l’affirmation, il faut tout de même avouer que résoudre en une ligne certains problèmes d’apparences très difficiles a quelque chose de… magique.

Alors, forcément, dans le domaine, on pourrait en imaginer beaucoup, chacun aura son avis sur la question. D’ailleurs, certains trouveront de la beauté dans certaines preuves que d’autres jugeront absolument inélégantes : tout n’est que subjectif et relatif.

Voici, en tout cas, trois problèmes et leurs solutions que je trouve, pour ma part, fort élégantes ! Faites chauffer les méninges !

Le puzzle impossible ?

Drapeau vert : Cette partie ne demande aucune connaissance mathématique particulière

Celui-ci ne prendra que peu de place, puisque je lui ai consacré toute une vidéo que vous devriez aller voir, si ce n’est déjà fait. Le principe est de recomposer une forme donnée à l’aide de 5 tetrominos (autrement dit, des pièces formées de 4 cases carrées).

Le chien coureur

Drapeau vert : Cette partie ne demande aucune connaissance mathématique particulière

Deux personnes, que nous nommerons Alphonse et Bernadette, A et B pour les intimes, se trouvent à 2 kilomètres l’une de l’autre et chacune marche en direction de l’autre à une vitesse approximative de 1 m/s. A côté d’Alphonse se trouve un chien qui s’élance vers Bernadette en même temps qu’Alphonse commence sa marche.

Sauf qu’un chien, ça ne prend pas son temps celui-ci trace en effet sa route à environ 5 m/s. Une fois arrivé au niveau de Bernadette, il repart en sens opposé retrouver Alphonse, toujours à la même vitesse, et fait ainsi des allers-retours jusqu’au moment où Alphonse et Bernadette se croisent.

Quelle est alors la distance totale parcourue par le chien ?

Il court, il court, le chienchien…

En se lançant tête baissée dans ce genre de problèmes, on peut se retrouver vite désemparé : il faut faire la somme de tous les déplacements de l’animal, avec des distances qui varient après chaque étape. En développant les calculs, on se trouve alors avec une série géométrique assez classique, et je laisse le soin aux lecteurs habitués de vérifier que je ne dis pas de bêtises.

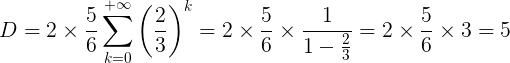
Voilà, voilà…

Eh oh, t’avais dis que c’était un drapeau vert, c’est quoi ce bazar ?

Oui, j’y viens, mais d’abord, commentons toutefois un petit peu cette formule :

• Le 2 correspond aux 2 kilomètres qui séparent A et B au début.
• Le 5/6 vient du fait que le chien va 5 fois plus vite que les personnages. S’il se dirige vers Alphonse, il couvre 5/6 de la distance tandis qu’Alphonse fait le 1/6 restant dans le même temps.
• A chaque fois que le chien croise un personnage, il fait demi-tour. La distance entre Alphonse et Bernadette a alors diminué d’un tiers – je vous laisse les calculs hein.

Bon, enfin, c’est bien joli tout ça, mais est-ce que ce ne serait pas prendre le canon pour tirer sur une mouche ?

Raisonnons mieux : Puisque nos deux personnages vont à la même vitesse, ils se croiseront pile à mi-distance. Ils auront fait 1 kilomètre chacun. Le chien allant 5 fois plus vite que chacun d’eux, il en aura fait 5 fois plus… soit 5 kilomètres…

Tadam !

Des graphes connexes

Drapeau jaune : Cette partie demande quelques connaissances mathématiques de base et un peu d’abstraction pour être entièrement saisie.

Pour l’exemple suivant, il faudra un peu plus de travail, mais rien d’insurmontable.

Donnons d’abord quelques définitions :

• Un graphe (non orienté), c’est simplement un ensemble de points – appelés sommets –  reliés par des traits, que l’on nomme des arêtes. Pour faire simple, on va supposer qu’il ne peut pas y avoir plusieurs traits qui joignent deux même points, et qu’un point ne peut pas être lié à lui-même par un trait. Dans les faits, ça ne change rien, mais autant faire simple.
• On dit qu’un graphe est connexe si l’on peut passer de n’importe quel point à n’importe quel autre en empruntant les arêtes du graphe

Le graphe de gauche n’est pas connexe : on ne peut pas, par exemple, aller d’un sommet rouge à l’autre en passant par les arêtes du graphe.

• Enfin, nous en aurons besoin, si on se donne un graphe, appelé G, on définit son complémentaire de la manière suivante : c’est le graphe G* avec les mêmes sommets, et deux sommets sont liés dans G* si et seulement s’ils ne le sont pas dans G. C’est une définition aux airs compliqués mais qui ne casse pas des briques quand on le voit graphiquement. En gros, c’est le graphe qui complète le graphe de départ.

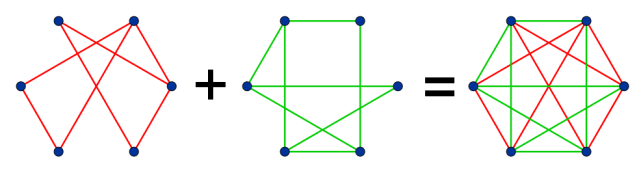
Le graphe tracé en vert est le complémentaire de celui en rouge. Ensemble, ils forment un graphe complet dont les arêtes sont soit vertes, soit rouges (mais aucune n’a les deux couleurs à la fois).

Alors, voilà donc la question : on se fixe un nombre de sommets supérieur ou égal à 4, noté n : existe-t-il plus de graphes connexes ou non connexes ayant n sommets ?

On pourrait essayer de les compter, de les dénombrer, et alors, la réponse serait toute donnée. Hélas, ce n’est pas une affaire aisée… Remarquons que la question ne demande pas le nombre exact de graphes connexes ou non connexes, simplement la catégorie la plus remplie.

Alors ? Une idée ?  Pas de triche hein ?

Réglons ce problème avec un argument massue : le complémentaire de tout graphe non connexe est connexe !

Admettons un instant cette propriété. En d’autres termes, si on a un graphe non connexe, on peut lui associer un graphe connexe, à chaque fois différent : il y a donc au moins autant de graphes connexes que de non connexes.

Pour terminer la preuve il suffit donc de trouver un graphe connexe dont le complémentaire est lui même connexe et le tour sera joué. Et cela fonctionne puisque nous avons pris au moins 4 sommets : il suffit de relier les points en formant une « ligne » non fermée.

Allez, le tour est presque joué. Oui parce que quand je parle d’une propriété, il faut bien la prouver tout de même, vous n’allez pas non plus gober tout ce que je dis, si ?

Alors voilà, prenons donc un graphe non connexe, que l’on appelle allègrement G, et montrons que son complémentaire est connexe. Prenons deux points, nommés x et y, dans ce graphe complémentaire.

• S’il n’était pas possible de passer de x à y dans le graphe d’origine, alors x et y seront liés par une arête dans le graphe complémentaire.
• Au contraire, s’il était possible de passer de x à y dans le graphe d’origine, alors il va falloir s’aider d’un troisième point. En l’occurrence, nous choisirons un point z qui n’est pas relié à x par un chemin (et donc, pas relié à y non plus, sinon on pourrait passer de z à y puis de y à x, et donc de z à x.). Ceci est possible car notre graphe de départ n’est pas connexe, rappelons-le. Alors, dans le graphe complémentaire, z est relié à x d’une part et à y d’autre part. Il est donc possible de passer de x à y en empruntant les arêtes du graphe complémentaire.

En bref, pour n’importe quel couple de points (x,y) du graphe complémentaire, on peut passer du premier au deuxième en passant par les arêtes. Bref, notre graphe complémentaire est connexe.

Le tour est joué !

Pour compléter

Encore plus de démonstrations élégantes ? En voici !

• Le Professeur Culture Précieuse vous propose de trouver le plus court chemin possible pour installer un magasin.
• Eljj passe en revue des démonstrations du célèbre théorème de Pythagore.
• Le livre Raisonnements Divins : quelques démonstrations mathématiques particulièrement élégantes de M. Aigner et G.M Ziegler.