Drapeau jaune : Cet article demande quelques connaissances mathématiques et un peu d’abstraction pour être entièrement compris

En arithmétique, les nombres premiers sont incontournables. Pour rappel, un entier positif est dit « premier » s’il possède exactement deux diviseurs entiers positifs – à savoir 1 et lui-même. C’est le cas de 2, 3, 5, 7, 11… mais pas de 1, puisqu’il n’a qu’un seul diviseur.

Derrière cette définition simpliste se cachent les briques élémentaires, les atomes des nombres entiers : en effet, n’importe quel entier positif peut se décomposer de manière unique en produit de nombres premiers. 10 = 2 x 5, 24 = 2 x 2 x 2 x 3, 2183 = 37 x 59, et ainsi de suite…

Cette propriété importante – qui porte tout de même l’appellation méritée de Théorème fondamental de l’arithmétique – est par exemple à la base de la cryptographie RSA, laquelle vous permet de faire des achats sur Internet sans (trop) risquer de vous faire voler votre numéro de carte bancaire. En l’occurrence, le procédé fait intervenir deux très grands nombres premiers multipliés entre eux pour donner un nombre encore plus grand.

Adi Shamir, Ron Rivest et Len Adleman, fondateurs de la cryptographie RSA

Casser le code RSA (et donc, s’emparer des données bancaires planétaires) revient donc plus ou moins à faire l’opération inverse : à partir de ce très grand nombre, retrouver les deux nombres premiers qui ont servi à le composer. Évidemment, on pourrait tester tous les nombres jusqu’à trouver le bon, mais on parle là de très grands nombres, et une méthode aussi brute prendrait des années avant de produire un résultat satisfaisant…

Bref, les nombres premiers, c’est bien, c’est utile et c’est fun. Nous savons beaucoup de choses sur ces nombres fantastiques, mais en ignorons beaucoup d’autres. Parmi les domaines de recherche se pose ainsi la question de la répartition de ces nombres premiers.

Ce que l’on sait : une histoire d’infini

Euclide (gravure)

Il existe une infinité de nombres premiers : ce résultat est connu depuis Euclide et ses Eléments, 300 ans avant notre ère.

Les nombres premiers sont en plus grande quantité que toute quantité proposée de nombres premiers.

Euclide, Eléments

Une démonstration de ce résultat consiste à supposer le contraire : si l’on suppose que les nombres premiers existent en nombre fini, alors en les multipliant tous ensemble et en ajoutant 1, on obtient un nouveau nombre premier, ce qui rend donc notre hypothèse absurde. Le plus grand nombre premier connu à ce jour est le nombre 2^74 207 281 – 1, qui possède près de 22 millions de chiffres !

Cela dit, il y en a beaucoup, mais il y en a aussi de moins en moins. En 1896, Jacques Hadamard et Charles-Jean de la Vallée Poussin démontrent un résultat conjecturé par Gauss et Legendre : si l’on considère un nombre entier N, alors la proportion de nombres premiers compris entre 1 et N se rapproche, à mesure que N grandit, de la quantité 1/ln(N), une quantité qui tend lentement mais surement vers 0.

Si l’on utilise cette approximation, on trouve que 8.7 % des entiers entre 1 et 100 000 sont premiers (soit 8000 environ). Entre 1 et 100 000 000, on tombe à 5.4 %.

Ce résultat fait au passage intervenir l’analyse complexe, et notamment la fonction zêta de Riemann qui nécessitera sans doute un article pour elle seule.

En gros, les nombres premiers sont, d’une certaine manière, de plus en plus rares à mesure que l’on avance dans notre ensemble des nombre entiers, et en plus, il existe des écarts entre nombres premiers aussi grands que l’on veut. Prenons le nombre 100! (le produit 1 x 2 x 3 x … x 99 x 100). Ce nombre est un multiple de tous les entiers de 1 jusqu’à 100. Par conséquent :

• 100! + 2 est la somme de deux multiples de 2, c’est donc aussi un multiple de 2
• 100! + 3 est un multiple de 3
• …
• 100! + 100 est un multiple de 100

Ainsi, nous avons 99 nombres consécutifs qui ne sont pas premiers – et qui sont, certes, très grands. Naturellement, le raisonnement que nous avons eu avec 100 tient aussi avec 1000, 10000, ou n’importe quel entier. On peut donc trouver des suites de plus en plus grandes d’entiers consécutifs qui ne soient pas premiers.

Jumeaux, cousins, sexys…

Il existe des écarts aussi grands que l’on veut, c’est un fait. Mais en existe-t-il de toutes les tailles ? Si la réponse est évidemment non pour 3, 5, 7 ou tous les nombres impairs, que dire de 2, 4, 6…?

Deux nombres premiers dont la différence vaut 2 s’appellent des nombres premiers jumeaux. C’est le cas de 3 et 5, de 5 et 7, de 11 et 13, et de beaucoup d’autres couples de nombres premiers. Le 25 décembre 2011, suite au projet PrimeGrid, on a pu identifier les nombres 3 756 801 695 685 × 2^666 669 + 1 et 3 756 801 695 685 × 2^666 669 – 1 comme étant des nombres premiers jumeaux. A titre purement informatif, ces deux nombres possèdent plus de 200000 chiffres dans leur écriture décimale.

A vrai dire, on soupçonne qu’il existe une infinité de ces couples, mais personne n’a pu le prouver à ce jour. D’ailleurs, on soupçonne également qu’il existe une infinité de couples de nombres premiers dont la différence vaut 4, qu’on appelle nombre cousins. Aussi, on pense qu’il existe une infinité de couples de nombres premiers dont la différence vaut 6, aussi appelés nombres sexys.

En fait, pour n’importe quel entier pair supérieur ou égal à 2, on a conjecturé qu’il existe une infinité de couples de nombres premiers dont la différence vaut ce nombre : cette supposition est connue sous le nom de Conjecture de Polignac.

Absolu inconnu avant son article sur les espaces entre nombres premiers, Yitang Zhang a connu un extraordinaire et soudain gain de notoriété !

En 2013, Yitang Zhang parvient toutefois à démontrer que ce résultat est au moins vrai pour un entier compris entre 2… et 70 000 000 ! En clair, il existe une valeur comprise entre 2 et 70 000 000 pour laquelle il existe une infinité de couples de nombres premiers dont la différence vaut cette valeur. Et n’allez pas croire qu’il s’agit là d’un petit résultat : 70 millions peuvent paraître grands, mais il s’agit d’un minuscule grain de poussière sur l’échelle astronomique des nombres entiers.

On pourrait par ailleurs s’intéresser aux écarts qui « reviennent le plus souvent » avant un entier donné. Si nous listons tous les nombres premiers entre 1 et 100, nous obtenons

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Regardons maintenant les écarts entre les nombres premiers successifs.

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8

Ici, l’écart qui apparait le plus souvent est le 2 : c’est notre champion sauteur – comme baptisé par John Conway – des nombres premiers de 1 à 100. Si nous poussions jusqu’à 101, 2 et 4 seraient présents en même proportion. Passé 947, c’est le nombre 6 qui règne en maître, et ce jusqu’à… au moins 10¹² ! Quant à la suite, les mathématiciens pensent que le nombre 30 deviendra le nouveau champion sauteur, puis ce sera le tour de 210, 2310…

Qu’ont-ils de si incroyables ? Si on écrit leur décomposition, voici ce que l’on voit

• 6 = 2 x 3
• 30 = 2 x 3 x 5
• 210 = 2 x 3 x 5 x 7
• 2310 = 2 x 3 x 5 x 7 x 11

Ces nombres sont en réalité les produits des plus petits nombres premiers : on les appelle des nombres primordiaux. Ainsi, les champions sauteurs, hormis le nombre 4 qui apparaît parfois, seraient les nombres primordiaux !

Ce résultat est très dépendant d’une autre conjecture, celle de Hardy-Littlewood. Sous réserve que cette conjecture soit vraie, Paul Erdős a réussi à prouver que les champions sauteurs devenaient de plus en plus grands, tendant même vers l’infini.

Des conjectures qui résistent

Et bien d’autres résultats restent à démontrer…

En 1850, Tchebychev a réussi à démontrer une conjecture établie par Bertrand qui affirmait qu’entre n’importe quel nombre entier et son double, on pouvait trouver un nombre premier. Par exemple, entre 8 et 16, on trouve le nombre premier 11. Entre 26 et 52, on trouve le nombre 37.

D’autres résultats de ce genre, plus fins, n’ont pas encore été démontrés. C’est le cas de la conjecture de Legendre,

Conjecture de Legendre : pour tout entier n, il existe un nombre premier entre n² et (n+1)².

Par exemple, en prenant n = 1000, cette conjecture affirme qu’il existe un nombre premier entre 1 000 000 et 1 002 001 (et en effet, on pourrait par exemple citer 1 000 003, 1 000 211 ou 1 001 191). A ce jour, on a seulement pu montrer qu’entre ces bornes, il existait un nombre premier ou semi-premier – produit de deux nombres premiers distincts, comme 11 x 13, 17 x 3, etc…

Nous pourrions également citer la conjecture d’Andrica,

Si p_n désigne le n-ième nombre premier, alors √p_n+1-√p_n < 1

En gros, si on a un nombre premier, inutile d’aller chercher un autre nombre trop loin. Mais là encore, une preuve ou un contre-exemple restent encore à trouver !

La spirale d’Ulam

La répartition des nombres premiers a quelque chose de mystérieux, presque inaccessible. Pourtant, lorsque l’on s’amuse à les dessiner, il en sort des phénomènes très ordonnés, comme celui de la spirale d’Ulam, du nom de ce mathématicien qui, s’ennuyant à écouter une conférence qui ne l’intéressait guère, se mit à griffonner sur sa feuille de papier.

Le principe est simple : il suffit, en commençant pas le 1 au centre du dessin, d’enrouler les nombres entiers autour de ce 1.

Puis, on entoure ou on colorie les nombres premiers, et on regarde ce que l’on obtient.

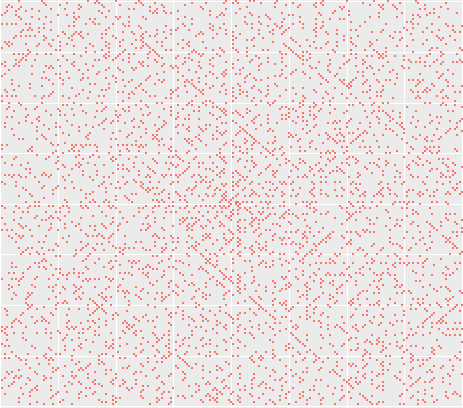
Vous distinguerez peut-être certaines lignes obliques sur cette figure. Ces alignements correspondent à des polynômes de degré 2, de la forme an² + bn + c, qui donnent un grand nombre de nombres premiers dès lors que l’on remplace n par un entier.

Le mathématicien Euler s’est d’ailleurs intéressé  à ces nombres chanceux, c’est-à-dire les entiers p tel que le nombre n² + n + p soit premier si l’on remplace n par 1, 2, 3… et ainsi de suite jusqu’à p-2. 17 est un exemple de ceux-ci, et l’on peut voir sur la spirale l’alignement des 15 nombres premiers que ce polynôme engendre.

Il ne faut toutefois pas espérer trouver une formule qui permette de générer les nombres premiers en un clin d’oeil : le semblant d’ordre que nous observons est aussi relatif que subjectif. Mais avouez que ça a tout de même de l’allure !

Pour compléter

• Science étonnante aborde la première et la deuxième conjecture de Hardy-Littlewood… qui s’avèrent en fait incompatibles !
• Eljj parle de la spirale d’Ulam et de la spirale de Sacks
• La Spirale d’Ulam toujours, sur le site Nombres – Curiosités, théories et usages
• Sur Blogdemaths, comment reconnaître deux nombres premiers jumeaux
• Les divagations mathématiques de Ian Stewart, qui parle des champions sauteurs.
• En anglais, les vidéos de Numberphile sur la spirale d’Ulam, les nombres premiers jumeaux, les grands sauts entre nombres premiers, les travaux de Yitang Zhang…
• En anglais aussi, l’article sur les « Jumping Champions«