Drapeau vert : Cet article ne demande aucune connaissance mathématique particulière

<hr /Tout ne peut pas être démontré, c’est un fait prouvé rigoureusement, mathématiquement. De tous les énoncés vrais qu’il peut exister, certains ne pourront jamais obtenir de preuve. Ces énoncés, on s’attend à ce qu’ils soient forcément compliqués à comprendre pour le commun des mortels. Les mathématiques souffrent déjà de ce stéréotype qui veut qu’elles soient forcément difficiles à saisir, mais si même les plus brillants mathématiciens ne parviennent pas à démontrer ou infirmer des propositions qui proviennent de leur propre univers, alors où va le monde ? Pourtant, il existe au moins un problème à l’énoncé très simple et pourtant encore auréolé de mystère : la conjecture de Syracuse.

Mise en situation

Choisissez un nombre entier strictement positif. S’il s’agit d’un nombre pair, divisez-le par 2. S’il est impair, multipliez-le par 3 et ajoutez 1. Continuez ainsi avec le nouveau nombre obtenu pour obtenir ce que l’on nomme une suite de Syracuse. Par exemple, si nous partons du nombre 13 :

• 13 est impair, on doit le multiplier par 3 et ajouter 1, on obtient 40.
• 40 est pair, on le divise par 2, on obtient 20.
• 20 est pair, on le divise par 2, on obtient 10. On divise 10 par 2 pour obtenir 5.
• 5 est impair, il faut le multiplier par 3 puis ajouter 1 pour obtenir 16, et ainsi de suite. Si l’on regarde les différentes étapes de notre suite, on obtient les nombres suivants :

13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1…

Il semblerait que nous nous retrouvons dans un cycle 4, 2, 1 qui continue jusqu’à l’infini. Prenons alors un autre nombre entier et construisons sa suite de Syracuse, par exemple 42 :

42, 21, 64, 32, 16, 8, 4, 2, 1, 4, 2, 1…

Encore une fois, nous aboutissons à ce cycle 4, 2, 1. Plus exactement, dès que l’on atteint le chiffre 1, alors la suite n’est qu’une succession de ces nombres 4, 2 et 1. Voilà notre conjecture.

La conjecture de Syracuse

Peu importe le nombre de départ choisi, la suite de Syracuse atteint le chiffre 1 (et donc boucle sur le cycle 4, 2, 1).

Cet énoncé porte le nom de « Conjecture » et non de théorème, ce qui signifie qu’un tel résultat n’a pas été démontré pour tous les nombres entiers.

Nous pouvons alors nous amuser à regarder ces suites de Syracuse et certaines de leurs propriétés, notamment :

• leur temps total de vol, c’est-à-dire le nombre d’étapes avant d’arriver à 1
• leur altitude maximale, soit le plus grand nombre atteint par la suite

Même en partant de nombre peu élevés, il est possible d’obtenir des altitudes très hautes. Voici par exemple la courbe donnée par les étapes successives de la suite de Syracuse en partant de 31.

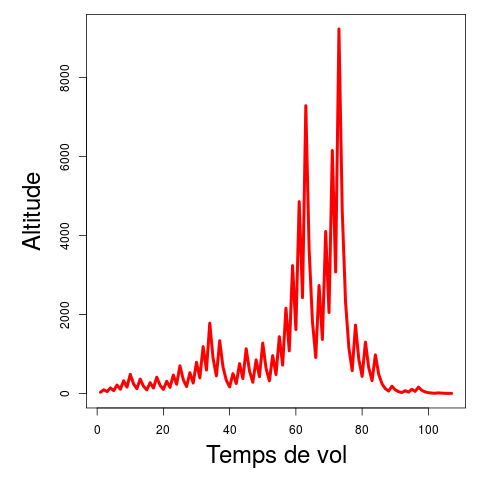
Trajectoire d’une suite de Syracuse qui part du nombre 31. Elle atteint une altitude maximale de 9232

On obtient alors une durée de vol de 107 et une altitude maximale de 9232, rien à voir avec les pauvres petits exemples de ce début d’article. Au contraire, on peut prendre des nombres très grands et voir leur altitude chuter de manière vertigineuse sans jamais voler plus haut que le point de départ. Voici l’exemple en partant du nombre 1000000 (1 million) :

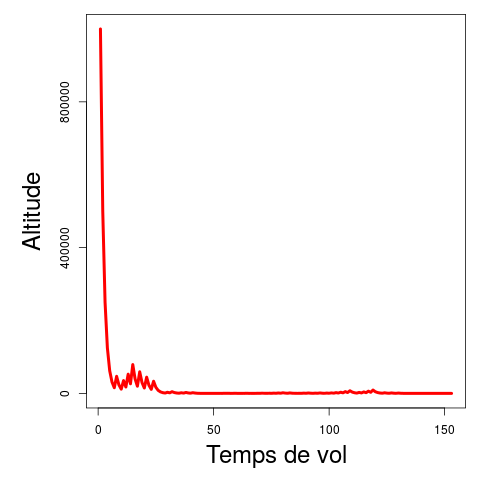
Trajectoire d’une suite de Syracuse qui part du nombre 1000000. L’altitude chute de manière vertigineuse au début du vol.

On s’aperçoit qu’il n’existe vraisemblablement pas de lien direct entre la grandeur d’un nombre et son altitude ou sa durée de vol. Bien entendu, il est possible de construire des suites de Syracuse qui possèdent une altitude aussi grande que l’on veut (il suffit alors de commencer par un très grand nombre), et il est aussi possible de construire des suites au vol aussi long que possible. En effet, en prenant un nombre de la forme 2ⁿ, alors on sait que sa durée de vol sera de n étapes. Néanmoins, ces puissances de 2 augmentent très vite avec n. Par exemple, on sait que 2²⁰ = 1048576 et que l’on aura 20 étapes en partant de ce nombre. Ce n’est pourtant pas la peine d’aller aussi loin pour trouver des vols aussi long, puisque 37 fournit déjà un vol d’une durée de 107 étapes.

La question pourrait alors être de déterminer, pour un nombre d’étapes données, le plus petit nombre duquel partir pour obtenir de nombre d’étapes.

Arbre de Syracuse

Partons du nombre 1 et raisonnons à l’envers : comment est-il possible de l’atteindre ? Pour celui-ci, il faut forcément avoir été au nombre 2 à l’étape d’avant. Pour atteindre 2, il faut forcément avoir été à 4, et donc avoir été à 8 avant, et à 16 l’étape encore avant.

En revanche, pour atteindre l’altitude 16, on peut provenir de l’altitude 32 – dans ce cas, on divise par 2, et on obtient bien 16 – ou de l’altitude 5 – et ici, on devra multiplier par 3 et ajouter 1 pour obtenir 16.

5 et 32 sont donc à la même altitude, et on peut encore remonter pour voir comment ces nombres ont pu être obtenus, et ainsi de suite. On peut construire alors un graphique, que l’on nomme arbre de Syracuse. Si l’on représente les nombres entiers par des points, deux points sont reliés entre eux s’il est possible de passer de l’un à l’autre en une étape de la suite de Syracuse.

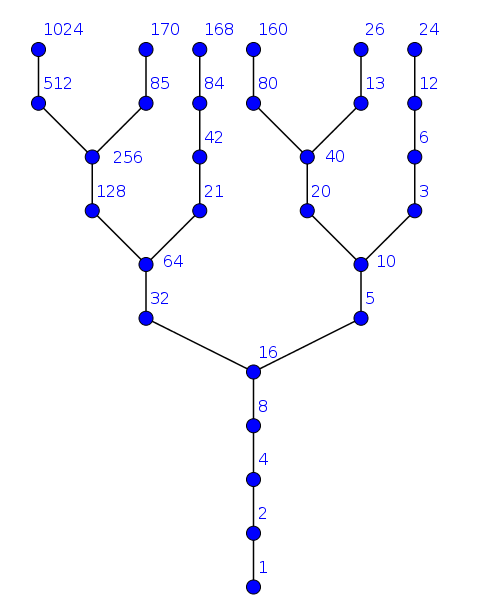
Arbre de Syracuse de profondeur 11

En représentant l’arbre de cette manière, on peut voir que tous les points qui se situent au même niveau, à la même distance du 1 auront une durée de vol égale. Il suffit de descendre de l’arbre pour établir la suite de Syracuse qui correspond au nombre entier choisi.

A la lumière des commentaires précédents, il est évident que cet arbre possède une infinité de points. De même, si un entier apparaît dans cet arbre, alors il ne peut apparaître qu’une seule fois. La conjecture de Syracyse peut alors se réécrire de cette manière :

Tous les nombres entiers apparaissent dans l’arbre de Syracuse.

Seulement… Cela ne rend pas la conjecture plus simple à déterminer. Il existe toutefois certains arguments qui donnent une vague idée du comportement d’une telle suite en général.

Des débuts de preuve ?

Tout d’abord, notez que cette conjecture a été prouvée pour tous les nombres jusqu’à 100000000000000000000 (ou, autrement écrit, 10²⁰). Autant vous dire que si vous souhaitez trouver un contre-exemple, il va falloir voir du côté des grands nombres. Par ailleurs, si votre suite de Syracuse passe à un seul instant en dessous de ce seuil, vous pouvez être certain qu’elle finira par atterrir en 1.

Cette remarque étant faite, on ne s’intéresse donc désormais qu’aux très grands nombres. On peut alors remarquer que, lorsque le nombre que l’on considère est impair, si on le multiplie par 3 et que l’on ajoute 1, on obtient alors un nombre pair, qui sera alors divisé par 2. On va alors rassembler ces deux opérations en une seule : si un nombre est impair, alors on le multiplie par 3, on ajoute 1 et on divise par 2.

C’est ici que nos grands nombres interviennent : d’une part, que l’on ajoute 1 ou pas, ça ne change pas grand chose pour notre grand nombre : en gros, on le multiplie par 3/2, c’est-à-dire 1.5. D’autre part, on peut dire,à une étape donnée, que l’on a plus ou moins 50% de chance d’avoir un nombre pair et 50% de chance d’avoir un nombre impair. Dans le premier cas, on multiplie par 1.5, dans l’autre par 0.5 : en moyenne, toutes les deux étapes, on multiplie donc le nombre par 1.5 x 0.5 = 0.75, qui est plus petit que 1 : notre suite de Syracuse est donc décroissante.

Attention, en réalité, la suite de Syracuse n’est pas aléatoire, et ce genre de raisonnement ne peut donc pas lui être appliqué directement. Néanmoins, le résultat peut être interprété de la manière suivante : le gain d’un nombre impair est inférieur à la perte d’un nombre pair.

Si, plutôt que de multiplier par 3, on avait multiplié par 5, on aurait abouti à un comportement tout à fait différent, avec des suites qui tendraient vers l’infini.

D’autres avancées ont été faites : on sait que si on considère un nombre entier n suffisamment grand, alors le nombre de valeurs inférieures à n dont la suite de Syracuse atterrit en 1 est supérieur à n^0.81. Par exemple, parmi tous les entiers inférieurs ou égaux à 10³⁰, on sait qu’il y en a au moins (10³⁰)^0.81 – qui est environ égal à 2.10²⁴ – qui auront une suite de Syracuse qui tend vers 1. Ce n’est pas énorme en proportion (environ 0.000001 % pour notre cas), mais cela reste une avancée.

Le théorème sera démontré lorsque (ou si) le 0.81 de cette formule sera remplacé par 1. Qu’attendez-vous pour vous y lancer ?